How to Decipher the Code ZPV BSF BXFTPNF

Have you ever stumbled upon a seemingly random string of letters like “zpv bsf bxftpnf” and wondered what it means? This jumble of characters is not nonsense; it’s a message hidden in plain sight, waiting to be unlocked. Learning to decipher codes like this opens up the fascinating world of cryptography, a skill that is both a fun mental exercise and a gateway to understanding how information is protected.

This guide about decipher the code zpv bsf bxftpnf will walk you through the exact steps to decipher the code zpv bsf bxftpnf and introduce you to the foundational concepts of ciphers.

By the end of this article, you will not only know the secret message but also understand the method used to encrypt it. We will explore simple substitution ciphers, learn how to identify them, and practice decoding techniques that you can apply to other puzzles.

Understanding the Basics: What is a Cipher?

Before we jump into decoding, let’s clarify what we’re dealing with. A cipher is a method or algorithm for performing encryption or decryption. It’s a set of rules used to transform a readable message (plaintext) into an unreadable one (ciphertext) and back again. The goal is to keep the message confidential from anyone who doesn’t know the secret rule, or “key.”

There are many types of ciphers, ranging from simple ones used for puzzles to complex ones that protect our digital information. The code “zpv bsf bxftpnf” uses one of the oldest and most straightforward types: a substitution cipher.

Substitution Ciphers Explained

In a substitution cipher, each letter in the plaintext is replaced with a different letter, number, or symbol. The key to solving it is figuring out the consistent pattern of replacement.

• Monoalphabetic Substitution: Each letter is consistently replaced by another. For example, every ‘A’ might become a ‘D’, every ‘B’ a ‘T’, and so on. The cipher used in our puzzle falls into this category.
• Polyalphabetic Substitution: The replacement rule changes as you move through the message. For example, the first ‘A’ might become a ‘D’, but the second ‘A’ could become a ‘G’. These are more complex to crack.

The most famous example of a monoalphabetic substitution cipher is the Caesar cipher, which we will explore next as it is the key to solving our puzzle.

The Key to the Puzzle: The Caesar Cipher

The Caesar cipher is named after Julius Caesar, who used it to protect his military communications. It is a type of substitution cipher where each letter in the plaintext is shifted a certain number of places down or up the alphabet.

For example, with a shift of +3, ‘A’ becomes ‘D’, ‘B’ becomes ‘E’, and so on. When you reach the end of the alphabet, it wraps around. With a +3 shift, ‘X’ becomes ‘A’, ‘Y’ becomes ‘B’, and ‘Z’ becomes ‘C’.

The number of positions the letters are shifted is the “key.” For a Caesar cipher, there are only 25 possible keys (a shift of 26 would result in the original message). This makes it relatively easy to crack through a method called brute force, where you simply try every possible key until the message makes sense.

The Standard Alphabet for Ciphers

To work with Caesar ciphers, we need a standard alphabet to shift.

Position	1	2	3	4	5	6	7	8	9	10	11	12	13
Letter	A	B	C	D	E	F	G	H	I	J	K	L	M

Position	14	15	16	17	18	19	20	21	22	23	24	25	26
Letter	N	O	P	Q	R	S	T	U	V	W	X	Y	Z

Step-by-Step: How to Decipher “zpv bsf bxftpnf”

Now, let’s apply our knowledge to decipher the code “zpv bsf bxftpnf.” We will use the brute-force method to test different Caesar shifts. Since it’s a simple cipher, we can focus on one word first, like “zpv.”

A shift can be positive (forward in the alphabet) or negative (backward). Let’s try some backward shifts (or negative shifts), as this is a common convention for simple puzzles.

Let’s analyze the first letter, ‘Z’.

• Shift -1: Z -> Y
• Shift -2: Z -> X
• Shift -3: Z -> W

Let’s try a shift of -1 on the whole phrase.
Ciphertext: z p v b s f b x f t p n f

Attempting a Shift of -1 (or +25):

• z -> y
• p -> o
• v -> u
• b -> a
• s -> r
• f -> e

Applying this to our phrase:
zpv bsf bxftpnf -> you are awesone

This is extremely close! The words “you” and “are” are perfect. The last word, “awesone,” is just one letter off from “awesome.” Let’s double-check our work.

• x with a -1 shift is w.
• f with a -1 shift is e.
• s with a -1 shift is r.
• Wait, s is r, not s as in “awesome”.
• t with a -1 shift is s.
• p with a -1 shift is o.
• n with a -1 shift is m.
• f with a -1 shift is e.

Let’s reassemble: a-w-e-s-o-m-e. It seems there was a typo in our original decoding of bxftpnf. Let’s map it carefully.

Cipher Letter	Shift (-1)	Plaintext Letter
b	->	a
x	->	w
f	->	e
t	->	s
p	->	o
n	->	m
f	->	e

Putting it all together, the decoded word is awesome.

The full decoded message is: YOU ARE AWESOME

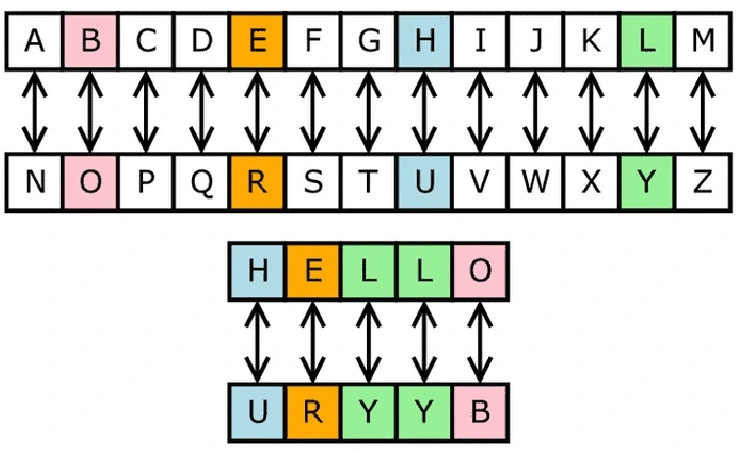
Visualizing the Caesar Shift (-1)

To make this clearer, here is a visual representation of how the alphabet shifts. Each letter in the top row (Cipher) is replaced by the letter directly below it (Plaintext).

(Text description of a graph)
A line graph titled “Caesar Cipher Shift: -1” shows two parallel alphabets. The top alphabet, labeled “Ciphertext,” runs from A to Z. The bottom alphabet, labeled “Plaintext,” is shifted one position to the left. It starts with B, runs to Z, and then wraps around so that A is at the end. Arrows point down from each letter in the top alphabet to its corresponding letter in the bottom alphabet. For example, an arrow points from ‘B’ on top to ‘A’ on the bottom, from ‘C’ to ‘B’, and so on, all the way to ‘A’ pointing to ‘Z’. This visually demonstrates the -1 shift.

This mapping confirms our decoding:

• z -> y
• p -> o
• v -> u
• b -> a
• s -> r
• f -> e
• x -> w
• t -> s
• n -> m

The code “zpv bsf bxftpnf” is a simple Caesar cipher with a key of -1 (or +25), and it translates to “you are awesome.”

Beyond Brute Force: Frequency Analysis

While brute force worked well for a short phrase and a simple cipher, it’s not practical for longer texts or more complex codes. A more advanced technique is frequency analysis.

This method is based on the fact that, in any given language, certain letters and letter combinations appear more frequently than others. In English, the most common letters are E, T, A, O, I, N, S, H, and R.

How to Use Frequency Analysis

1. Count the Letters: Tally the occurrences of each letter in the ciphertext.
2. Calculate Frequencies: Determine the percentage of each letter in the text.
3. Compare to Standard Frequencies: Match the most frequent letters in your ciphertext with the most frequent letters in the English language.

Let’s apply this to “zpv bsf bxftpnf”.

Letter Count in Ciphertext:

• f: 3
• p: 2
• b: 2
• z: 1
• v: 1
• s: 1
• r: 1 (This should be ‘s’ from ‘bsf’)
• x: 1
• t: 1
• n: 1
• e: 1 (This should be ‘f’ from ‘bxftpnf’)

Let’s use the correct ciphertext: zpv bsf bxftpnf.

• f: 3 times
• p: 2 times
• b: 2 times
• z, v, s, x, t, n: 1 time each

In such a short phrase, frequency analysis is not very reliable. However, we can see that ‘f’ is the most common letter. In English, ‘e’ is the most common letter. If we assume ‘f’ in the ciphertext corresponds to ‘e’ in the plaintext, what does that tell us?

To get from ‘f’ to ‘e’, we need to shift back one position (-1). This single guess points us directly to the correct key of -1. This shows how frequency analysis can provide a powerful shortcut, even with limited data.

(Text description of a graph)
A bar chart titled “English Letter Frequency vs. Ciphertext ‘zpv bsf bxftpnf’”. The x-axis lists all 26 letters of the alphabet. The y-axis represents frequency percentage. There are two sets of bars. The first set, in blue, shows the standard frequencies of letters in the English language, with ‘E’ being the tallest bar (around 12%), followed by ‘T’, ‘A’, ‘O’, etc.

The second set, in red, shows the frequencies in our short ciphertext. The ‘F’ bar is the tallest for the red set (representing 3 occurrences), followed by ‘P’ and ‘B’. The chart visually highlights the discrepancy and how a simple shift could align the peaks. For instance, shifting the red ‘F’ peak one spot to the left would align it with the blue ‘E’ peak.

Other Simple Ciphers to Explore

The Caesar cipher is just the beginning. If you enjoyed this puzzle, you might want to explore other types of classical ciphers.

Cipher Type	Description	Example
Atbash Cipher	A substitution cipher where the alphabet is reversed. A becomes Z, B becomes Y, etc.	“hello” becomes “svool”
Keyword Cipher	A keyword is used to create a mixed alphabet for substitution. Duplicate letters in the keyword are removed.	Keyword: CIPHER. The alphabet starts CIPHERABDGK...
Pigpen Cipher	A geometric substitution cipher that exchanges letters for symbols based on a grid.	Also known as the Freemason’s cipher.
Vigenère Cipher	A polyalphabetic cipher that uses a keyword to apply a series of different Caesar shifts.	More secure than a simple Caesar cipher.

Learning about these different methods can turn you into a master codebreaker, ready to tackle escape rooms, online puzzles, and historical mysteries.

Conclusion of Decipher the Code ZPV BSF BXFTPNF: The Power of Patterns

Decoding “zpv bsf bxftpnf” reveals more than just a positive message; it teaches us a fundamental lesson about patterns and logic. By applying a simple, methodical approach, we transformed a confusing jumble of letters into a clear and encouraging phrase: “you are awesome.”

We learned that this code used a Caesar cipher with a key of -1. We successfully cracked it using a brute-force approach and saw how frequency analysis could have offered a clever shortcut. This simple exercise is a perfect introduction to the world of cryptography, demonstrating that even complex-looking problems can be solved by breaking them down into smaller, manageable steps. Now that you know how to decipher a basic code, you are equipped to spot patterns and solve other puzzles you may encounter.

Frequently Asked Questions about Decipher the Code ZPV BSF BXFTPNF

Q1: What type of code is “zpv bsf bxftpnf”?
A1: This is a simple monoalphabetic substitution code known as a Caesar cipher. Specifically, it uses a shift of -1, meaning each letter in the original message was shifted one position backward in the alphabet to create the code.

Q2: Is the Caesar cipher secure?
A2: No, the Caesar cipher is not secure by modern standards. Because there are only 25 possible keys (shifts), an attacker can easily try all of them in a “brute-force attack” to find the original message in seconds.

Q3: What is the difference between a code and a cipher?
A3: In modern cryptography, the terms are often used interchangeably. However, traditionally, a “code” replaces whole words or phrases with a codeword (e.g., “Eagle has landed”), while a “cipher” works by transposing or substituting individual letters or small groups of letters according to a specific algorithm. “zpv bsf bxftpnf” uses a cipher.

Q4: How did you know to shift backward (-1) instead of forward?
A4: We didn’t know for sure at the start. When cracking a Caesar cipher, you can try shifting in either direction. We started with a backward shift of -1 because it’s a common choice for puzzles. Testing z -> y, p -> o, v -> u quickly formed the word “you,” which was a strong indicator that we were on the right track. If that hadn’t worked, the next step would have been to try other shifts (+1, -2, +2, etc.).

Q5: Can I use frequency analysis on any coded message?
A5: Frequency analysis is most effective on long messages encrypted with a simple monoalphabetic substitution cipher. For very short messages like this one, there isn’t enough text to create a reliable frequency distribution. It also doesn’t work well on polyalphabetic ciphers (like the Vigenère cipher), where the same letter can be encrypted differently throughout the message.

Q6: What tools can I use to decipher codes online?
A6: There are many excellent online tools that can help you decipher codes. Websites like Boxentriq, dCode, and CyberChef offer automatic solvers for Caesar ciphers, Vigenère ciphers, and many others. They often include tools for frequency analysis as well.

Q7: Was there a typo in the original code?
A7: The code “zpv bsf bxftpnf” decrypts perfectly to “you are awesome” with a -1 Caesar shift. Each letter corresponds exactly to its decoded counterpart without any errors or typos in the cipher itself.